数値の丸め方、標準数
※ この二つの規格は製図には直接関係しないが、ハンドブックに掲載されており、知
っていると役に立つこともあるのでそのまま紹介しておきます。
数値の丸め方
JIS Z 8401
序文 省略
１. 適用範囲 この規格は、鉱工業において用いる十進法の数値の丸め方について規定
する。
備考 省略
２. 数値の丸め方
ａ） 丸めるとは、与えられた数値を、ある一定の丸めの幅の整数倍がつくる系列の中
から選んだ数値に置き換えることである。この置き換えた数値を丸めた数値と呼
ぶ。
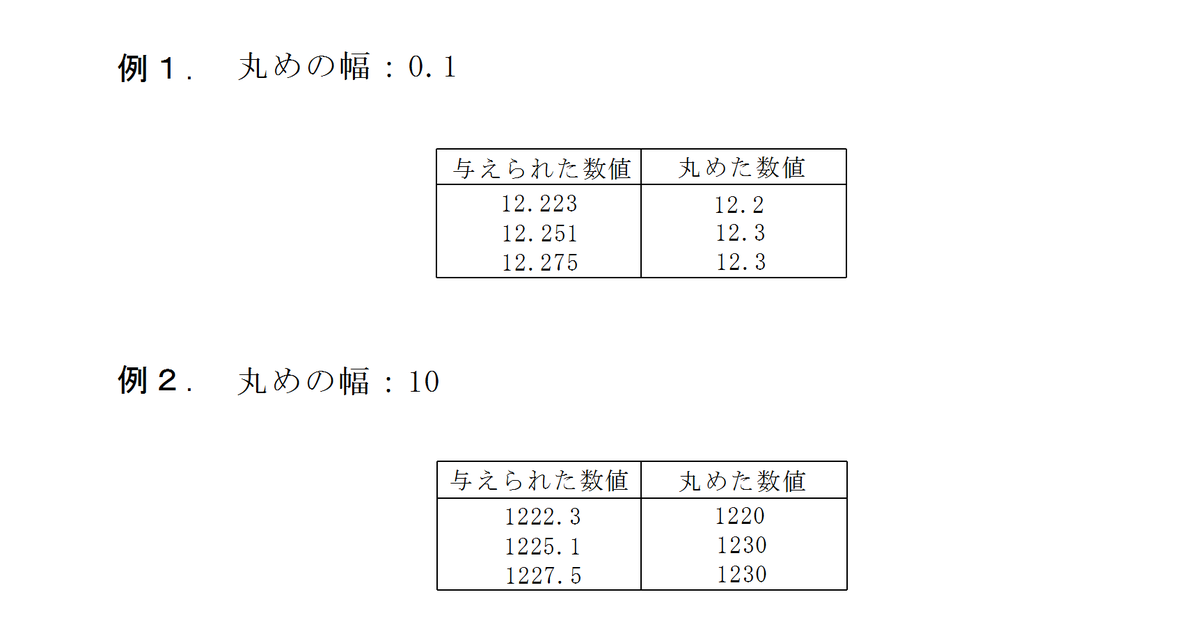
例１. 丸めの幅：0.1
整数倍：12.1，12.2，12.3，12.4 ･･･
例２. 丸めの幅：10
整数倍：1210，1220，1230，1240 ･･･
ｂ） 与えられた数値に最も近い整数倍が一つしかない場合には、それを丸めた数値と
する。
ｃ） 与えられた数値に等しく近い、二つの隣り合う整数倍がある場合には、次の規則
Ａが用いられる。
規則Ａ 丸めた数値として偶数倍のほうを選ぶ。
備考 規則Ａには、例えば、一連の測定値をこの方法で処理するとき、丸めによる
誤差が最小になるという特別な利点がある。
参考１． ｃ）の場合、次の規則Ｂが用いられることもある。
規則Ｂ 丸めた数値として大きい整数倍のほうを選ぶ。
２. 規則Ｂは、電子計算機による処理において広く用いられている。
３. 丸めの幅をｄ×（d、κ は整数、ただし、1≦d≦9）とすれば、有効数字は
丸めた数値の以上の位の数字列としてあらわす。例えば、丸めの幅を
＝0.01 とすれば、以上の位、すなわち、小数点以下２位までの数字列が
有効数字となる。
４. 丸めの幅を10×（κ は整数）とすれば、規則Ｂはいわゆる四捨五入である。
なお、丸めの幅を5×（κ は整数）とした二捨三入・七捨八入も特定の分野
で用いられている。
５. この規格では対象となる数値として正の数値しか想定していない。負の数
値を対象とする場合は、その絶対値に適用しなければならない。
ｄ） 規則Ａ、Ｂを２回以上使って丸めることは、誤差の原因となる。したがって、丸
めは、常に１段階で行わなければならない。
例 12.251 は、12.3 と丸めるべきであって、まず、12.25とし、次いで12.2 とし
てはならない。
ｅ） 規則Ａ，Ｂは、丸めた数値の選び方について何の考慮すべき基準もない場合だけ
適用すべきである。安全性の要求又は一定の制限を考慮しなければならないとき
は、例えば、常に一定方向へ丸めるほうが良いことがある。
ｆ） 丸めの幅を表示することが望ましい。
標 準 数
JIS Z 8601
１. 総 則
１.１ 適用範囲 この規格は、工業標準化・設計などにおいて数値を定める場合に、
選定の基準として用いる標準数について規定する。
１.２ 標準数の定義 標準数とは付表に示す数値であって、10の正 又は負の整数ベ
キを含み、公比がそれぞれ 、
、
、
、および
である等比数列の
各項の値を実用上便利な数値に整理したものである。
これらの数列をそれぞれ Ｒ５、Ｒ10、Ｒ20、Ｒ40、Ｒ80、の記号で表す。
１.３ 用語の意味 この規格で用いる主要な用語の意味は、つぎのとおりとする。
（１） 基本数列 Ｒ５、Ｒ10、Ｒ20、Ｒ40 の数列。
（２） 特別数列 Ｒ80 の数列。
（３） 理 論 値 10 の正または負の整数ベキを含み、公比がそれぞれ
、
、
、
、
である等比数列の各項の値。
（４） 計 算 値 理論値を有効数字５ケタに整理して求めた数値。
（５） 増 加 率 標準数の各数列内における、ある数値からつぎの数値に移ると
きの増加する割合。
２. 標準数の使用方法
２.１ 工業標準化・設計などにおいて、段階的に数値を定める場合には標準数を用
い、単一の数値を定める場合でも標準数から選ぶようにする。
２.２ 選ぶべき標準数は、基本数列の中で増加率の大きい数列から採る。すなわち、
Ｒ５、Ｒ10、Ｒ20、Ｒ40 の順で用いる。なお、基本数列によれない場合にだけ特別数
列を用いる。
２.３ 標準数の適用に際して、ある数列をそのまま用いることができないときはつぎ
のようにして用いる。
（１） いくつかの数列を併用する ある範囲全部を同一の数列から採ることがで
きない場合には、その範囲を必要に応じていくつかに分け、それぞれの範
囲に対し最も適した数列を選んで用いる。
（２） 誘導数列として用いる ある数列のある数値から２つ目、３つ目、
･･････、Ｐ個目ごとにとって用いる。この場合の数列を誘導数列という。
なお、２，３，･･･、Ｐをピッチ数という。
（３） 変位数列として用いる ある数列によってきめられた特性に関係ある他の
特性の数値を、同じ数列から採ることができないときに、この特性に適し
た数値を含む他の数列を選び、これを元の特性に等しい増加率をもつ誘導
数列にしたものを用いる。この場合の数列を変位数列という。
（４） 計算値を用いる 標準数よりもさらに正確な数値を必要とする場合には、
これに対応する計算値を用いる。
３. 標準数列の記号
３.１ 標準数列の記号は、範囲を示す必要のない場合１.２に規定した数列記号をそ
のまま用い、範囲を示す必要のある場合、数列記号のつぎにかっこをつけてその範囲を
示す。
例：Ｒ10（1.25･･･） Ｒ10数列で1.25以上のもの。
Ｒ20（･･･45） Ｒ20数列で45以下のもの。
Ｒ40（75･･･300） Ｒ40数列で75以上300以下のもの。
３.２ 誘導数列の記号は、つぎのようにする。
誘導数列を求めた元の数列記号／ピッチ数（誘導数列に含まれる１つの数値）
なお、範囲を示す必要のある場合は３.１に準ずる。
例：Ｒ10/3（･･･80･･･） Ｒ10数列から３つ目ごとに採ったもので８０を含む
もの。
Ｒ5/2（１･･･1600） Ｒ5数列から2つ目ごとに採ったもので、１以上1600
以下のもの。
３.３ 変位数列の記号は３.２に準ずる。
例：Ｒ20/4（1.12･･･） Ｒ20数列から4つ目ごとにとった1.12以上のもの
で、その増加率はＲ5と等しい。
Ｒ80/8（25.8･･･165） Ｒ80数列から8つ目ごとにとった25.8以上165以下
のもので、その増加率はＲ10と等しい。
備 考 １. 付表の標準数の数値に 10 の正 または 負の整数ベキをかけたものも標準数とする。
2. 配列番号の使い方 基本数列における標準数の計算（¹）には、付表に示された配列番号を用い
れば、つぎのような計算ができる。
注（¹） 配列番号によって計算を行った場合は、標準数と理論値との差に相当する誤差をと
もなう。
（１） 標準数の積 ２つの標準数 Ｎ₁、Ｎ₂ の積に相当する標準数を求めるには、（Ｎ₁に対応す
る配列番号）＋（Ｎ₂に対応する配列番号）の数値に等しい配列番号をもつ標準数を付表
から読み取る。
例：3.15 × 1.6 の計算
配列番号の和＝20 + 8 ＝28
配列番号 28 に対応する標準数＝5＝（ 3.15 × 1.6 に相当する標準数）
（２） 標準数の商 ２つの標準数 Ｎ₁、Ｎ₂ の商に相当する標準数を求めるには、（Ｎ₁に対応す
る配列番号）－（Ｎ₂に対応する配列番号）の数値に等しい配列番号をもつ標準数を付表
から読み取る。
例：4.25 ÷ 25 の計算
配列番号の差＝25 － 56 ＝－31
配列番号 －31 に対応する標準数＝0.17＝（ 4.25/25 に相当する標準数）
（３） 標準数のベキ 標準数Ｎの正の整数ベキに相当する標準数を求めるには、（Nに対応する
配列番号）×（Nのベキ指数）の数値に等しい配列番号をもつ標準数を付表から読み取
る。
例： ( 1.18 )² の計算
配列番号とベキ指数の積＝ 3 × 2 ＝ 6
配列番号 6 に対応する標準数＝ 1.4 ＝（ 1.18² に相当する標準数）
（４） 標準数の乗根 標準数Ｎの乗根に相当する標準数を求めるには、（Nに対応する配列番
号）÷（Nの根指数）の値が整数ならば、この値に等しい配列番号をもつ標準数を付表か
ら読み取る。
例： の計算
配列番号と根指数の商＝（－32 ）÷ 2 ＝－16
配列番号 ー16 に対応する標準数＝0.4＝（ に相当する標準数）
※ 理論的に正確な寸法でない場合は、数値は四捨五入することが多い。普通はこれで
特に問題になることはないであろう。
しかし四捨五入では、数値は大きいほうに偏りが出る傾向があるらしい。安全性から
はこれでよいのだが、大量生産の場合は都合が悪い場合がおこる。詳しくは数値の丸め
方で検索してみてください。いろいろな解説がされています。
標準数も、寸法を決める場合、何の拠り所もない場合は、これを検討したほうが良
い。同じく標準数で検索すれば、いろいろ参考になることが出てくる。
ちなみに、標準数の記号で使われるＲは、これを考案したフランス人のルナールから
きている。標準数はルナール数とも呼ばれる。
